第八課 大綱
甲 多項式的基本概念
乙 多項式的四則運算
丙 餘式定理
丁 因式定理
多項式
基本概念
- 多項式：$f(x) = a_nx ^ n + a_{n-1}x^{n-1} + … + a_1x + a_0$
- $n$為正整數或零，$a_n$、$a_{n-1}$、…、$a_{1}$、$a_{0}$為實數
- 項：$f(x)$的$n$次項為$a_nx ^ n$，$n-1$次項為$a_{n-1}x^{n-1}$，…，$1$次項為$a_{1}x$，常數項為$a_{0}$
- 係數：$f(x)$的$x ^ n$次項係數為$a_n$，$x^{n-1}$次項係數為$a_{n-1}$，…，$x$次項係數為$a_{1}$，常數項係數為$a_{0}$
- 次數
- 若$a_nx ^ n$為次數最高的非零項，則$f(x)$的最高次方為$n$，又記deg$f(x) = 3$，稱$f(x)$為$n$次多項式，$a_n$為$f(x)$首項係數(領導係數)
- 多項式的值：$f(a)$的值即為拿$a$帶入$f(x)$
- $n$為正整數或零，$a_n$、$a_{n-1}$、…、$a_{1}$、$a_{0}$為實數
四則運算
加法
- 相同項係數相加就對了
減法
- 相同項係數相減就對了
乘法
-
兩個乘開你不會嗎
-
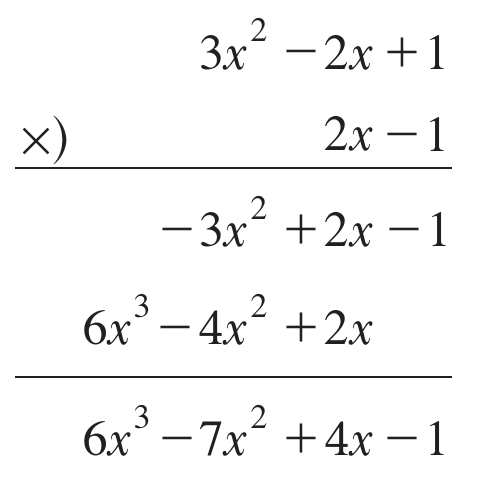
即使係數為$0$一樣要留空間
除法
-
長除法打天下
-
即使係數為$0$一樣要留空間
-
餘式一定要小於商式
綜合除法
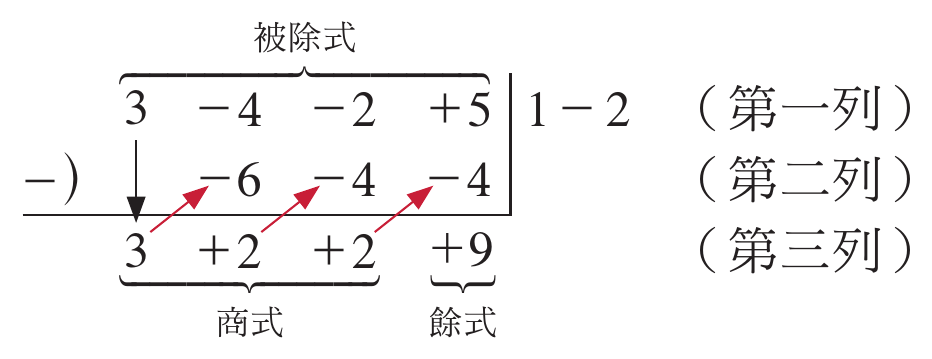
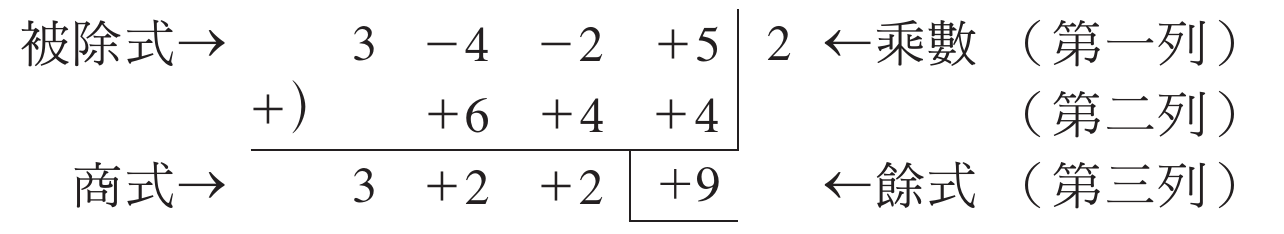
- 展開
將$3x^3 + 2x^2 - x + 5$以$(x-1)$展開
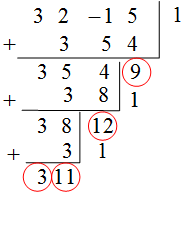結果：$3(x-1)^3 + 11(x-1)^2 + 12(x-1) + 9$
除法原理
$f(x) = g(x) * q(x) + r(x)$
$f(x)$為被除式，$g(x)$為除式，$q(x)$為商式，$r(x)$為餘式
餘式定理
$f(x) = g(x) * q(x) + r(x)$
且$g(x) = (ax - b)$
於是餘式$r(x) = f(\frac{b}{a})$
因式定理
設$f(x)$為一多項式，若$ax-b$為$f(x)$之因式，即$f(x) = (ax-b) \times q(x)$，
則$f(\frac{b}{a}) = 0$