第三課 大綱
3-1 對物體運動的研究歷程
3-2 牛頓運動定律
3-3 天體運動
克卜勒行星運動定律
過程
- 地心說擁護者第谷觀星後留下大量數據遇證實地心說未果
克卜勒 運用資料證實日心說
第一定律:橢圓定律
- 內容:行星繞太陽的軌道為一橢圓,且太陽位於橢圓的其中一個焦點上
- 近日點、遠日點
- 軌道上有一點與太陽最近,稱為近日點
- 軌道上有一點與太陽最遠,稱為遠日點
- $\small軌道半徑 = \frac{近日距 + 遠日距}{2}$
第二定律:面積定律
- 內容:
{同一顆,備註:很愛考,red} 行星與太陽的連線,在相同時間內掃過相同的面積,即其面積速率相等 - 應用:近日點處軌道速率最快,遠日點處軌道速率最慢
- 近日點與遠日點切向速率和近日距與遠日距成反比
- $\small 面積速率 = \frac{A}{\Delta t_1} = \frac{B}{\Delta t_2}$
第三定律:週期定律
- 內容:繞太陽的所有行星,其軌道半徑立方與其公轉週期的平方為一定值
- $\frac{{R_1}^3}{{T_1}^2} = \frac{{R_2}^3}{{T_2}^2} = … = K$
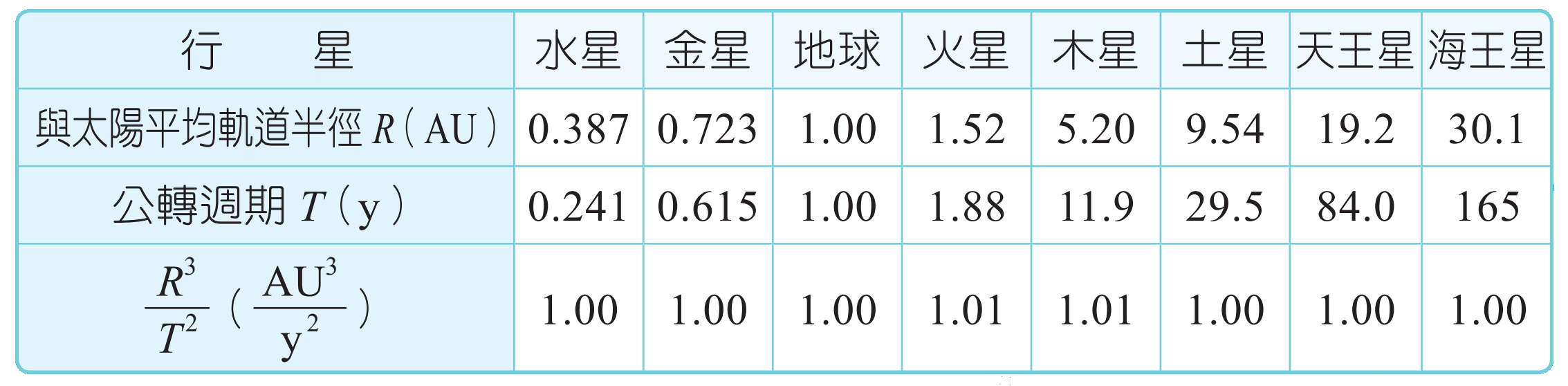
- 延伸:繞同一天體的所有天體也皆符合週期定律
例:月球和人造衛星繞地球的$\frac{{R}^3}{{T}^2}$相等
演繹法與歸納法
- 牛頓推倒出三大行星定律概念
- 從第二運動定律出發,提出:若物體受到向心作用,則該物體運動必會滿足面積定律
- 滿足面積定律做等速率圓周運動的物體,若滿足克卜勒第三運動定律,所受向心力會與半徑平方成反比
- 從第二運動定律出發,提出:若物體受到向心作用,則該物體運動必會滿足面積定律
| 名稱 | 演繹法 | 歸納法 |
| 解釋 | 由基本的定律或公理出發,經過合理的推導,得出正確結果的方法 | 從觀測或實驗的資料出發,不加任何假設,找出現象後隱藏的共同規律 |
| 人物 | 牛頓 | 克卜勒 |